はじめに
さて、しばらくの間、下記のヒストグラム(CLOSE-OPEN)が、どのような分布で近似できるか検討してきましたが、なかなか良い分布が見つかりませんでした。
そこで、tick-volumeのヒストグラムに視点を変更してみました。すると、そのヒストグラムは、対数正規分布がマッチすることが分かりました。

また、時間単位で作成されている足(データ)をtick数単位にまとめ直した足(データ)ではどうなるか?
確認しました。すると、正規分布がマッチすることが分かりました。
※1分足をtick数でまとめて加工したデータ

そこで、,まとめるtick数を変化させた場合の偏差を求めてみると、下図のドットが現れました。
次に、そのドットに近似させる式を探したところ、ランダムウォークの拡散現象(分散)を表す式(上)のt(時間)をtick_volumeに置き換えた式であることがわかりました。また、拡散係数を便宜上ルートの外に出すと、下記の通りの式となりマッチさせることが出来ました(緑色のライン)。ちなみにα=2.24

※t:時間 / tc:tick_volume

ここまでをまとめてみると・・・
- ドル円の単位時間当たり(今回は、H1)のボラティリティ(CL-OP)のヒストグラムに単独でマッチするような分布は見つけられなかった。しかし、tick_volumeをまとめて作成したヒストグラムが正規分布となり、かつ、tick_volumeのヒストグラムが対数正規分布となっていることが解った。そのことから、偏差が異なる正規分布の集合(合成)が、あのような分布を形作るという結論となった。
- ランダムウォークの拡散現象(分散)を表す式をtick_volumeに置き換えた式を用い、偏差とtick_volumeの関係を数式化することができることがわかった。
tick_volumeの予測
さて、ここから本題です。偏差とtick_volumeの関係がわかれば、ticl_volumeを予測することにより偏差を予測することが可能ではないか?と考え、tick_volumeを予測してみることにしました。まずは、チャートのtick_volumeを観察してみます。(今回は、USDJPY & EURUSDのH1を使用しています。)
ジ~と見ます。wすると、1日単位で周期的に変化している様に見えます。そこで、次の様に仮定してみます。
【各時間毎のtick_volumeは、各時間の固有パラメータと直前のtick_volumeの出来高に影響を受ける。】
これを式にすると。。

※a[0]~a[23]:各時間に割り当てられるパラメータ
ここまで仮定すれば、後は重回帰を用いて最適解を求めれば出来上がりです。まずは、結果からご覧ください。赤の折れ線が予測値で水色が、tick_volumeです。表示期間は、2014/05/29~06/04で、最適化の期間は、2014/05/01から1000barsです。
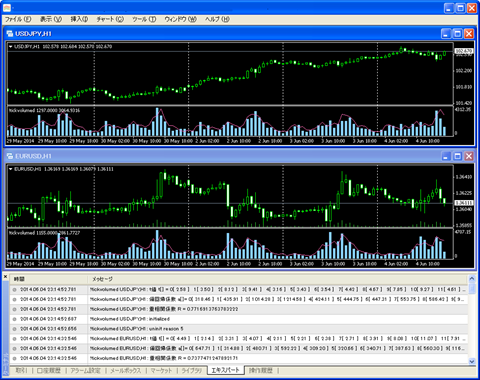
うまくマッチしているように見えるのですが如何なものでしょうか(・・?
今回テストしたモノは、MT4がMT5の仕様に対応したこともありMT5用のヘッダーをお借りして作成してみました。
ココよりDLが可能です。
DL出来るファイルは、以下の通りです。(今回は、DLL未使用にしてみました。)
┣Matrix.mqh 【Matrix operations library - library for MetaTrader 5】から取得し一部加工しました。(行列用)
┣Multiple_Regression_Analysis.mqh (重回帰用)
┗TKVP_H1.mq4 (テスト用のインジケータ)
ボラティリティの予測
次に、予測したtick_volumeを用いて1σを表示させてみました。(白線:1時間後 青線:2時間後)
tick_volumeの予測値が結果より若干高くなっているためか、1σの範囲が若干広い気もしますが。。
課題
パラメータの不足TKVP_H1.mq4 を作動させてもらうとわかると思いますが、予測値が結果と大きく乖離する場合があります。それは、イベント(指標の発表、要人の発言、市場の休場など)が原因です。イベントを取り入れるパラメータが必要だと思われます。
拡散係数の計算
tickデータから直接計算できれいいのですが、M1を使用しているのでまとめる時に誤差が生じてしまいます。
良い方法があればいいのですが、今回は、単純にvolumeの加算による方法をとりました。


4 件のコメント :
凪の状態を観測し、
カタストロフィの状態を観測し、
凪の状態のパラメータでカタストロフィの状態が包含出来ないのであれば、
カタストロフィ状態を表現する分布を再定義する必要がありますよね。
やはり別物ですので、其れなりの表現が必要ですね。
はじめましてTORA-sanと申します。いつも楽しみにBlogを拝見させていただいております。
上記の分布の件ですが、尖度の高いものは、
もしかするとフォークト関数でフィット出来るかもしれません。
亀レスなので既に解決済みでしたらスルーしてください。
TORA-sanさんへ
はじめまして^^;
フォークト関数(ガウスとコーシ―分布の混合分布?)ですか?なるほど勉強させていただきます。φ(..)メモメモ ありがとうございます。
前に一度、コーシー分布は、試したことがあったのですが、非常に扱いづらかったので止めてしまいました^^;(フットテール部分のデータがあるかないかで大きく分布の形状が変化してしまい、期待する結果が得られませんでした。あと、分散の定義がないというのも扱いづらくて。。。)
神功皇后さんへ
反論しようかといろいろと考えていましたが、よい結果が得られませんでした^^;やはり似て非なる物と考えた方が良いのかもと考えたりもしています。
一番の理由は、拡散係数がうまく処理できない事。。 もしかした動的な物か?。。。と。。。
Lévy flight試しましたか??安定分布の。
コメントを投稿