忘却型相関係数

2012/10/29修正しました。

相関係数は、非常に計算コストの高い関数で、私の様な非力なPCを使っている者にとっては、リアルタイムで随時処理していくには不向きなものだと思っています。ということで、近似関数を用いて相関係数の計算コスト削減を行ってみました。

変換

まずは、相関係数の公式の確認です。対象となるデータをxとyとし期間をnとすると以下のようになります。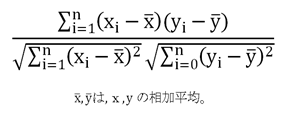

この公式の分母と分子にそれぞれ1/nを乗算すると、以下のようになります。

ここで、各項を見ると相加平均であるのがわかります。そこで、見慣れた記号SMAに置き換えて見ると

となります。そこで、SMAをEMAで置き換えると（近似させると）、

となり、EMAの公式を当てはめると以下のようになります。

これで忘却型相関係数の完成です。

確認作業

本来の相関係数と忘却型相関係数をコードにすると以下のようになります。
（※以下のコードは、値幅とティックボリュームの相関関係を求める場合です。）

//+------------------------------------------------------------------+
//|相関係数                                                               |
//+------------------------------------------------------------------+
int start(){
   double x,y,avx,avy,sigxy,sigx,sigy;
   int i,q;
   for(i=limit; i>=0; i--){
      // x:(High[i] - Low[i]) y:Volume[i];
      for(q=pd;q>0;q--){
      //xの加算
         avx += High[i+q-1] - Low[i+q-1];
      //ｙの加算
         avy += Volume[i+q-1];
      }
      //x.yの相加平均
      avx /=pd;
     avy /=pd;
      
      //変数の初期化
      sigxy =0;
     sigx   =0;
     sigy   =0;
      
      for(q=pd;q>0;q--){
         x = High[i+q-1] - Low[i+q-1];
         y = Volume[i+q-1];
         sigxy += (x-avx)*(y-avy);
         sigx   += (x-avx)*(x-avx);
         sigy   += (y-avy)*(y-avy);
      }
      cn[i] = sigxy/(MathSqrt(sigx)*MathSqrt(sigy));
      
   }
return(0);
}

//+------------------------------------------------------------------+
//|忘却型相関係数                                                          |
//+------------------------------------------------------------------+
int start(){
   double x,y;
   int    counted_bars=IndicatorCounted();
   if(counted_bars>0) counted_bars--;
   int limit=Bars-counted_bars-1;
   
   for(int i=limit; i>=0; i--){
      x      = High[i] - Low[i];
      y      = Volume[i];
      avx[i]   = (1-alfa)*avx[i+1] + alfa*x;
      avy[i]   = (1-alfa)*avy[i+1] + alfa*y;
      sigxy[i] = (1-alfa)*sigxy[i+1] + alfa*(x-avx[i])*(y-avy[i]);  
      sigx[i]  = (1-alfa)*sigx[i+1] + alfa*(x-avx[i])*(x-avx[i]);
      sigy[i]  = (1-alfa)*sigy[i+1] + alfa*(y-avy[i])*(y-avy[i]);
      //忘却型相関係数
      cn[i] = sigxy[i]/(MathSqrt(sigx[i])*MathSqrt(sigy[i]));
   }
return(0);
}
  

チャート上で確認すると,このようになります。

※チャート上のMAは、それそれの適用期間に合わせたSMAとEMAです。
※上記のサンプルをココに置いておきますので確認してみてください。

まとめ

本来、EMAは、忘却性能と逐次性能が有り、逐次型とか指数平均型とかのネーミングが良いのでしょうが、忘却という響きが好きで、忘却型としました。また、今回は、わかりやすいようにバッファを多用しましたが、１つ前の値しか使用しないので変数（static)で十分対応できます。
ChangeFinder、SDARモデルなどで検索すると、この手法の発展系を見ることが出来ます。