変換
まずは、相関係数の公式の確認です。対象となるデータをxとyとし期間をnとすると以下のようになります。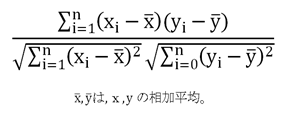
この公式の分母と分子にそれぞれ1/nを乗算すると、以下のようになります。

ここで、各項を見ると相加平均であるのがわかります。そこで、見慣れた記号SMAに置き換えて見ると

となります。そこで、SMAをEMAで置き換えると(近似させると)、

となり、EMAの公式を当てはめると以下のようになります。

これで忘却型相関係数の完成です。
確認作業
本来の相関係数と忘却型相関係数をコードにすると以下のようになります。(※以下のコードは、値幅とティックボリュームの相関関係を求める場合です。)
//+------------------------------------------------------------------+ //|相関係数 | //+------------------------------------------------------------------+ int start(){ double x,y,avx,avy,sigxy,sigx,sigy; int i,q; for(i=limit; i>=0; i--){ // x:(High[i] - Low[i]) y:Volume[i]; for(q=pd;q>0;q--){ //xの加算 avx += High[i+q-1] - Low[i+q-1]; //yの加算 avy += Volume[i+q-1]; } //x.yの相加平均 avx /=pd; avy /=pd; //変数の初期化 sigxy =0; sigx =0; sigy =0; for(q=pd;q>0;q--){ x = High[i+q-1] - Low[i+q-1]; y = Volume[i+q-1]; sigxy += (x-avx)*(y-avy); sigx += (x-avx)*(x-avx); sigy += (y-avy)*(y-avy); } cn[i] = sigxy/(MathSqrt(sigx)*MathSqrt(sigy)); } return(0); }
//+------------------------------------------------------------------+ //|忘却型相関係数 | //+------------------------------------------------------------------+ int start(){ double x,y; int counted_bars=IndicatorCounted(); if(counted_bars>0) counted_bars--; int limit=Bars-counted_bars-1; for(int i=limit; i>=0; i--){ x = High[i] - Low[i]; y = Volume[i]; avx[i] = (1-alfa)*avx[i+1] + alfa*x; avy[i] = (1-alfa)*avy[i+1] + alfa*y; sigxy[i] = (1-alfa)*sigxy[i+1] + alfa*(x-avx[i])*(y-avy[i]); sigx[i] = (1-alfa)*sigx[i+1] + alfa*(x-avx[i])*(x-avx[i]); sigy[i] = (1-alfa)*sigy[i+1] + alfa*(y-avy[i])*(y-avy[i]); //忘却型相関係数 cn[i] = sigxy[i]/(MathSqrt(sigx[i])*MathSqrt(sigy[i])); } return(0); }チャート上で確認すると,このようになります。

※チャート上のMAは、それそれの適用期間に合わせたSMAとEMAです。
※上記のサンプルをココに置いておきますので確認してみてください。
まとめ
本来、EMAは、忘却性能と逐次性能が有り、逐次型とか指数平均型とかのネーミングが良いのでしょうが、忘却という響きが好きで、忘却型としました。また、今回は、わかりやすいようにバッファを多用しましたが、1つ前の値しか使用しないので変数(static)で十分対応できます。ChangeFinder、SDARモデルなどで検索すると、この手法の発展系を見ることが出来ます。
7 件のコメント :
こんばんは。
忘却することに意味がある (現在に近いほど重みを大きくしたい) のであれば別ですが、相関係数はインクリメンタルに計算できますので、計算コスト自体はそう高くないと思います。
v,x,y を配列、a,b を整数 (配列中のインデックス) とし、
S(v,a,b) := Σ[i=a~b; v[i]] # つまり、総和
M(v,a,b) := S(v,a,b) / (b-a+1) # つまり、相加平均
F(x,y,a,b) := Σ[i=a~b; (x[i] - M(x,a,b)) * (y[i] - M(y,a,b))]
# (共)分散や相関係数の分母分子に出てくる項の形
と定義します。
このとき、期間 1~n → 期間 2~n+1 での F の差分を計算すると、
F(x,y,2,n+1) - F(x,y,1,n) = (S(x,1,n) * S(y,1,n) - S(x,2,n+1) * S(y,2,n+1)) / n - x[1] * y[1] + x[n+1] * y[n+1]
が成り立ちます (単純に展開して整理するだけです)。
S(x,2,n+1) = S(x,1,n) - x[1] + x[n+1]
S(y,2,n+1) = S(y,1,n) - y[1] + y[n+1]
ですので、相関係数ρ = F(x,y) / sqrt(F(x,x) * F(y,y)) は、
割と簡単に (インクリメンタルに) 更新していけることが分かります。
初回を除いて、計算量 (演算回数) が期間の長さ n に依存しないのも嬉しい所です。
kartzさんへ
ご指摘ありがとうございます。
ほんとだ@@;。。
修正記事を作成します。
いつもありがとうございます^^;
kartzさんへ
申し訳ありませんが追記します。
ご指摘のあった部分をコード化する際に一つ疑問が浮かびました。
一般的な相関関数は、各相加平均が同値になるのに対し、各相加平均をインクリメンタルに計算した場合は、各相加平均が更新されるため一般的な相関関数と同値にならないような気がしますが、考え方が間違っているのでしょうか?
一般的な相関係数
F(x,y,1,n) := (x[1] - M(x,1,n)) * (y[1] - M(y,1,n))
+(x[2] - M(x,1,n)) * (y[2] - M(y,1,n))
+(x[3] - M(x,1,n)) * (y[3] - M(y,1,n))
:
:
:
+(x[n] - M(x,1,n)) * (y[n] - M(y,1,n))
インクリメンタルに計算した場合
F(x,y,1,n) := (x[1] - M(x,1,n)) * (y[1] - M(y,1,n))
+(x[2] - M(x,2,n+1)) * (y[2] - M(y,2,n+1))
+(x[3] - M(x,3,n+2)) * (y[3] - M(y,3,n+2))
:
:
:
+(x[n] - M(x,n,n+n-1)) * (y[n] - M(y,n,n+n-1))
相加平均をインクリメンタルに計算ぜずに初期値を使い続けるのが正解か?若しくは大勢に影響はないと考えるのが正解か?悩ましいところですが、どのように考えたほうが良いのでしょうか?
> インクリメンタルに計算した場合
> …
なぜこういう展開式になるのでしょうか??
F(x,y,1,n) なので、a=1, b=n で、M(*,a,b) → M(*,1,n) ですよ。
定義に沿って計算したものとインクリメンタルに計算したものが一致しない場合、
「インクリメンタルに計算できる」とは言いません。
以下のように計算すればいいのです。
結果は (実数計算の丸め誤差を除いて) 定義式に沿ったものと一致します。
MQL4 の配列インデックスとは逆順で、i = 1(最古), 2, … で書いています。
また、期間の長さが n で、a が決まれば b は決まるので、b は省略します。
定義に従って、S(x,1), S(y,1), F(x,x,1), F(y,y,1), F(x,y,1) を計算する。
ρ(x,y,1) ← F(x,y,1) / sqrt(F(x,x,1) * F(y,y,1))
for (i = 2; i <= last; i++) {
S(x,i) ← S(x,i-1) - x[i-1] + x[i+n-1]
S(y,i) ← S(y,i-1) - y[i-1] + y[i+n-1]
F(x,x,i) ← F(x,x,i-1) + (S(x,i-1) * S(x,i-1) - S(x,i) * S(x,i)) / n - x[i-1] * x[i-1] + x[i+n-1] * x[i+n-1]
F(y,y,i) ← F(y,y,i-1) + (S(y,i-1) * S(y,i-1) - S(y,i) * S(y,i)) / n - y[i-1] * y[i-1] + y[i+n-1] * y[i+n-1]
F(x,y,i) ← F(x,y,i-1) + (S(x,i-1) * S(y,i-1) - S(x,i) * S(y,i)) / n - x[i-1] * y[i-1] + x[i+n-1] * y[i+n-1]
ρ(x,y,i) ← F(x,y,i) / sqrt(F(x,x,i) * F(y,y,i))
}
念のため書き添えますが、コードにするときは、
j ← i - 1
k ← i + n - 1
などの中間変数を入れて、… - x[j] * y[j] + x[k] * y[k] 等にしてくださいね。
教えて頂きありがとうございます。
まるで、トンチンカンな事をやっていたようです。もう一度確認してみます。
kartzさんへ
ほぼ写経状態ですが、コード化に成功しました。まとめ次第、訂正させて頂きます。
ありがとうございました。
コメントを投稿