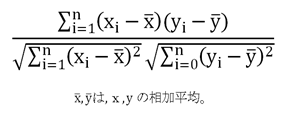2012/10/30追記
前回の内容にて、相関係数は、計算コストが高すぎてリアルタイムで随時処理していくには不向きなものと記述しましたが、kartzさんからコメントを頂き、それが誤りであったことがわかりましたので記述します。
内容は、私が説明するよりkartzさんのコメントを見て頂いた方が良いと思いますのでそちらをご覧ください。
※正直完全に理解できたか疑問が残るというのが本音だったりしますが。。(汗
コード化
kartzさんのコメントをコード化すると以下の様になりました。
//+------------------------------------------------------------------+
//| 相関係数_i.mq4 |
//| Copyright 2012, MetaQuotes Software Corp.|
//| http://www.metaquotes.net |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link "http://www.metaquotes.net"
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_color1 Yellow
extern int pd = 100;//期間
double Sx[]; //S(x,a,b) := Σ[i=a~b; x[i]]: xの総和
double Sy[]; //S(y,a,b) := Σ[i=a~b; y[i]]: yの総和
//M(v,a,b) := S(v,a,b) / (b-a+1): 相加平均
double Fxy[];//F(x,y,a,b) := Σ[i=a~b; (x[i] - M(x,a,b)) * (y[i] - M(y,a,b))]
double Fxx[];//F(x,x,a,b) := Σ[i=a~b; (x[i] - M(x,a,b)) * (x[i] - M(y,a,b))]
double Fyy[];//F(y,y,a,b) := Σ[i=a~b; (y[i] - M(x,a,b)) * (y[i] - M(y,a,b))]
double p[];//相加係数
//+------------------------------------------------------------------+
// | Custom indicator initialization function |
//+------------------------------------------------------------------+
int init() {
//---- indicators
IndicatorBuffers(6);
//---- drawing settings
SetIndexStyle(0,DRAW_LINE);
SetIndexStyle(1,DRAW_NONE);
SetIndexStyle(2,DRAW_NONE);
SetIndexStyle(3,DRAW_NONE);
SetIndexStyle(4,DRAW_NONE);
SetIndexStyle(5,DRAW_NONE);
SetIndexBuffer(0,p);
SetIndexBuffer(1,Sx);
SetIndexBuffer(2,Sy);
SetIndexBuffer(3,Fxy);
SetIndexBuffer(4,Fxx);
SetIndexBuffer(5,Fyy);
//----
return(0);
}
//+------------------------------------------------------------------+
//|初期値計算 |
//+------------------------------------------------------------------+
void Base(int index //開始位置
,int range //適用範囲
,double &S_x[] //Sx[];
,double &S_y[] //Sy[];
,double &F_xy[] //Fxy[];
,double &F_xx[] //Fx[];
,double &F_yy[] //Fy[];
){
int i;
double x,y,avx,avy,sigxy,sigx,sigy;
//x.yの相加平均
for(i=range;i>0;i--){
//xの加算
avx += High[index+i-1] - Low[index+i-1];
//yの加算
avy += Volume[index+i-1];
}
avx /=range;
avy /=range;
for(i=range;i>0;i--){
x = High[index+i-1] - Low[index+i-1];
y = Volume[index+i-1];
sigxy += (x-avx)*(y-avy);
sigx += (x-avx)*(x-avx);
sigy += (y-avy)*(y-avy);
}
S_x[index] = avx*range;
S_y[index] = avy*range;
F_xy[index] = sigxy;
F_xx[index] = sigx;
F_yy[index] = sigy;
}
//+------------------------------------------------------------------+
//|相関係数 |
//+------------------------------------------------------------------+
int start(){
double x,y,xn,yn;
int counted_bars=IndicatorCounted();
int limit=Bars-counted_bars -1;//2012/10/30変更
//初期設定
if(counted_bars<=0){
limit -=pd;//2012/10/30追記
Base(limit+1,pd,Sx,Sy,Fxy,Fxx,Fyy);
p[limit+1] = Fxy[limit+1]/MathSqrt(Fxx[limit+1]*Fyy[limit+1]);
}
for(int i=limit; i>=0; i--){
//追加項
x = High[i] - Low[i];
y = Volume[i];
//削除項(2012/10/30変更)
xn = High[i+pd] - Low[i+pd];//変更前 xn= High[i+pd+1] - Low[i+pd+1];
yn = Volume[i+pd]; //変更前 yn= Volume[i+pd+1];
//総和の更新
Sx[i] = Sx[i+1] + x -xn;
Sy[i] = Sy[i+1] + y - yn;
//F項の更新
Fxy[i] = Fxy[i+1] + (Sx[i+1]*Sy[i+1] - Sx[i]*Sy[i])/pd - xn*yn +x*y;
Fxx[i] = Fxx[i+1] + (Sx[i+1]*Sx[i+1] - Sx[i]*Sx[i])/pd - xn*xn +x*x;
Fyy[i] = Fyy[i+1] + (Sy[i+1]*Sy[i+1] - Sy[i]*Sy[i])/pd - yn*yn + y*y;
//相関係数
p[i] = Fxy[i]/MathSqrt(Fxx[i]*Fyy[i]);
}
return(0);
}
表示・確認
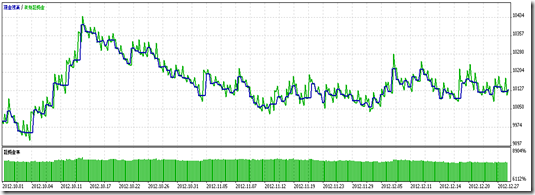
従来の計算方法で求めた結果を赤線で表示させ、今回の計算結果を黄線で重ね合わせてみました。
(変更前)
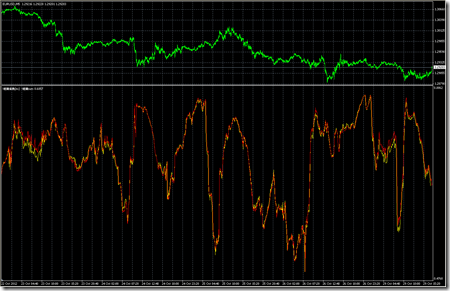
(変更後)※わかりやすくするために従来の計算方法を途中で終了させています。
まとめ
この方法なら、随時処理しても十分に使用できます。また、一つ勉強になりました。kartzさんありがとうございました。
//2012/10/30追記
kartzさんから指摘して頂いた、【削除項】の変更の結果、ほぼ一致したラインを作ることが出来ました。