対数正規分布を正規分布で見みる。
「対数正規分布を調べてみた。」では、対数正規分布で表示していましたが、正規分布で見てみると、以下の様になります。※タイムフレームは、M30です。
※この図の横軸は、対数化されています。
次の図は、上図の縦軸を対数化したものです。テールの部分に多少ズレはありますがうまくフィットしているように見えます。

ln(open[n-1]/open[n])*1000を試してみる。
本来は、ln(close[n-1]/close[n])*10000で行うそうですが、癖?自分の決まり?でopenを採用しました。※LN=lnです。ブログの性質上大文字になっています。
上記の図と同条件で表示させてみると、以下の様になりました。

また、同様に、縦軸も対数化下のが以下の図です。

全体的にフィットしていない様に見えます。また、特にテール部分が、フィットしていないのが気になります。もっとわかりやすくするために、正規分布(赤色)のデータを省いて表示させると、以下の様になります。
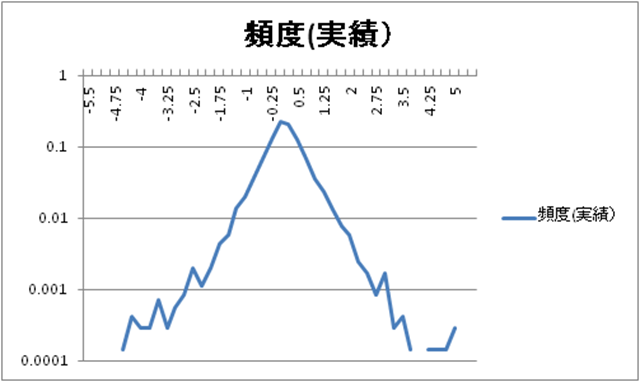
青色の線が2本の直線でできているように見えます。縦軸と横軸の両軸が対数化され、直線に見える分布と言えば、べき分布です。べき分布に関しては、以前にネタにしていますのでココを参考にしてください。前回は、絶対値を用いて検証したので、一本の線になっています。
タイムフレームを1Dにして同様に行ったのが以下の図です。

タイムフレームを上げると正規分布(横軸が対数化されたもの)に近づいた様に見えます。同様に縦軸を対数化し、青色の線のみ表示させると、青線が丸みを帯びてきていることが解ると思います。
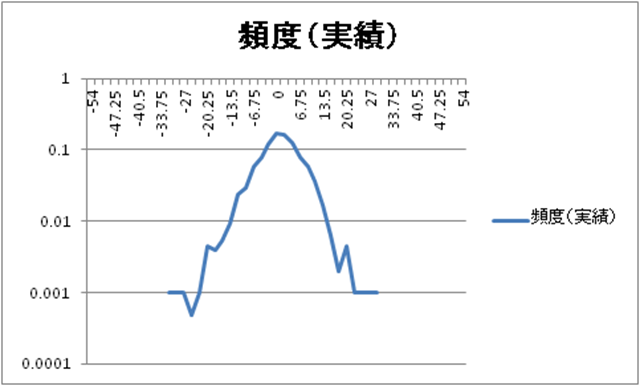
べき分布を調べた時と同じ現象です。
以下の図は、タイムフレームごとにまとめた図です。(以前作成した物)

その他
ln(高値/安値)*1000も試してみましたが、正規分布とは、ほど遠い結果となりました。図は、削除してしまいました。。orz 気になる方は、自作してみてください。
まとめ
便宜上ln(高値-安値)を使用していますが、窓が開いた時にうまく反映されない問題があります。その為、ATRのTRUE RANGEを使用したほうが良いと思います。上記の内容からリスクを見積る場合、低いタイムフレームで、ln(open[n-1]/open[n])*1000を使用するのは避けたほうがよさそうという結果になりました。